NYCJUG/2020-09-08
Meeting Agenda for NYCJUG 20200908
1. Beginner's Regatta: Calculating running times of music files. 2. Show and tell: a number puzzle. 3. Advanced topics: maybe too advanced. 4. Learning and teaching J: difficulty understanding array thinking -> Twitter? The value of a good community. 5. An item of interest: Paul Jackson talk on learning J on September 14th, 2020 at 10 AM PDT.
Beginner's Regatta
Say we are putting together a play list of songs in MP3 format and we want to know how long it will take to play the entire list of songs. So, we might have a list of the MP3 files like this:
>dir *.mp3 Volume in drive G is Music200821 Volume Serial Number is 3F0B-965F Directory of G:\ 04/07/2012 02:02 PM 1,671,119 000_The Baby Tree.mp3 07/19/2014 05:05 PM 5,359,910 010_Behind Blue Eyes.mp3 03/25/2012 10:35 PM 5,882,620 020_Lola.mp3 12/03/2004 10:02 AM 4,237,430 030_Bohemian Rhapsody - Queen.mp3 02/11/2012 04:15 PM 5,483,232 040_Working for the MTA.mp3 01/27/2013 02:23 PM 6,471,686 050_Johnny Law.mp3 05/20/2015 10:56 PM 4,598,694 060_Another Brick in the Wall, Pt. 1.mp3 12/03/2004 10:03 AM 2,018,706 070_We Will Rock You - Queen.mp3 07/21/2015 03:43 PM 5,223,698 080_Rolling.mp3 11/16/2011 01:02 PM 4,482,841 090_Bad Moon Rising.mp3 12/21/2015 11:45 PM 11,602,382 100_Wabash Cannonball.mp3 02/02/2013 07:01 PM 3,999,612 110_Shady Grove.mp3 04/01/2007 01:05 PM 4,845,038 120_Radar Love.mp3
We might start by supposing that the length of a piece of music is proportional to the size of its file. Here we divide the size of some randomly selected files (in KB) by the length in minutes and seconds.
szs=. 8438 6531 6365 4193 5496 3618 5434 |:tms=. 5 59,4 38,4 31,4 28,3 54,2 34,:2 53 NB. "|:" to display horizontally to make better use of screen space. 5 4 4 4 3 2 2 59 38 31 28 54 34 53 szs % 60#. tms NB. Convert times to seconds 23.5042 23.4928 23.4871 15.6455 23.4872 23.4935 31.4104
Unfortunately, these ratios vary by quite a bit. We might settle for picking a number near the middle and divide that into the total size of all the files.
(+/%#) szs % 60#. tms 23.503 348000%23.5 14808.5 0 60 60#:348000%23.5 NB. Seconds to hours, minutes, seconds 4 6 48.5106
How good is this approximation? Let's graph the actual times versus the estimated times, ordering them by estimates.
load 'plot'
ord=. /:szs%tms
'title Times vs. Estimates; key Time Estimate' plot ord{"1 (60#.tms),:szs%23.5
 We see that we underestimate at the low end and overestimate at the high end, so this is not a general solution.
We see that we underestimate at the low end and overestimate at the high end, so this is not a general solution.
Delving More Deeply into MP3
Once we look more deeply into MP3 encoding, we see that the file size alone is insufficient to estimate the time because MP3 files are encoded at different resolutions. That is, some recordings are of a higher quality than others because they encode the signal with more bits per second. A search of the web uncovered the command-line tool ffmpeg that extracts and displays information about MP3 files, including the duration.
Once installed, here is how we apply it to each file in question and extract the length of each song. First we experiment with extracting the duration information for a single file. We do this by creating a command-line template with the string "{flnm}" we will replace with the file name of each MP3 file.
cmd=. 'C:\Pgm\ffmpeg-20200824-3477feb-win64-static\bin\ffprobe "G:\{flnm}"'
$flnms=. 0{"1 dir 'G:\*.mp3'
90
{.flnms
+---------------------+
|000_The Baby Tree.mp3|
+---------------------+
We then run this for an example file and figure out how to extract the duration information for it.
$info=. shell cmd rplc '{flnm}';'000_The Baby Tree.mp3'
1882
I. ' Duration:' E. info
1758
#' Duration:'
11
11{.1769}.info NB. 1769=1758+11 - starting point+string length
00:01:44.4
We then apply this to all the files in our list and check that the results look correct:
whtms=. ,I.&>(<' Duration:') E.&.> info
tms=. 11{.&.>(11+whtms) }. &.> info
4{.tms
+-----------+-----------+-----------+-----------+
| 00:01:44.4| 00:02:53.1| 00:03:43.1| 00:03:29.6|
+-----------+-----------+-----------+-----------+
We want to convert these hh:mm:ss.ms (hour, minute, seconds) strings into number of seconds per song. Here's how we figure out how to do this; first we partition each time string on the colon character and convert the results to a numeric table:
".&><;._1 &> ':',&.>4{.tms
0 1 44.4
0 2 53.1
0 3 43.1
0 3 29.6
hms=. ".&><;._1 &> ':',&.>tms
If we sum this table, we get a three-element vector of hours, minutes, and seconds.
+/hms 0 259 2868
We first convert this into a number of seconds, then back into hours, minutes and seconds:
60#.+/hms 18408 0 60 60#:60#.+/hms 5 6 48
So we see that this 90-song play list has a running time of almost five hours and seven minutes.
Wrapping Up
Now that we have solved an example of the larger problem, let's wrap up the code, generalizing it a bit, to define a general-purpose routine to do this.
totalPlayTime=: 3 : 0
y=. endSlash y
cmd=. 'C:\Pgm\ffmpeg-20200824-3477feb-win64-static\bin\ffprobe "',y,'{flnm}"'
flnms=. 0{"1 dir y,'*.mp3'
info=. shell &.> (<cmd) rplc &.>(<'{flnm}');&.>flnms
keyStr=. ' Duration:'
whtms=. (#keyStr)+,I.&>(<keyStr) E.&.> info
tms=. ',' (]{.~]i.[) &.> whtms }.&.> info
hms=. ".&><;._1 &> ':',&.>tms
0 60 60#:60#.+/hms
)
We make the design decision to work on all .mp3 files given the name of the directory in which they reside. The "endSlash" utility ensures that our input directory name has a terminal slash character as this lends itself most readily to how we subsequently use it. We rely on a couple of standard utilities "dir" and "rplc" to list the .mp3 files in the directory and replace the place-holder "{flnm}" with each of the file names to build the list of commands we run using the "shell" utility.
We assign the key lookup string to a variable because we want to look past the label to the following text once we locate where the key string occurs. We generalize the extraction of the times from the remaining information by taking everything up to the first comma rather than relying on the hard-coded "11{." we used when figuring out how to do this.
Show-and-tell
Wasting time browsing Reddit, I found this problem: Find a number ABCDEFGHIJ such that A is the count of how many 0’s are in the number, B is the number of 1’s, and so on.
Being lazy, I figured the easiest way to find the answer was to write some J code. However, the search space is rather large as we might have to consider all 10-digit numbers. Briefly thinking about this, I realized that any such number beginning with zero could be eliminated but this still leaves something like nine billion cases. After some trial and error, I came up with the following:
tryAll=: 3 : 0
'st inc'=. y
nn=. st+i.inc NB. Some 10^.st-digit numbers
while. (1e10>{:nn) *. -.+./(] -: ' ' -.~ [: ": [: <: [: #/.~ '0123456789' , ])&>":&.>nn do.
nn=. nn+inc
end.
nn#~(]-:' ' -.~ [: ": [: <: [: #/.~ '0123456789' , ])&>":&.>nn
)
Given the large search space, this is written to loop through in reasonably sized pieces, say a million at a time. Eventually, after about six and a half hours, this returns a solution. However, while I was waiting for it to finish, I thought more about the problem and ended up solving it before the program gave a result. I won't spoil it completely but my reasoning started along these lines:
Since there are 10 digits in the result, the digits in the number must add up to 10.
Advanced Topics
I considered two advanced topics which are probably too complex to cover in a short section like this. These were "MicroKranen in J: an Embedding of the Relational Paradigm in an Array Language with Rank-Polymorphic Unification" and a J implementation of binary decision diagrams (BDD). However, in both cases the papers are fairly involved, though there is a video related to the BDDs that is somewhat interesting.
Binary Decision Diagrams
Binary decision diagrams are a data structure useful for representing Boolean functions. An overview of them can be found here. The main attraction seems to be that they can be thought of as a compressed representation of Boolean functions which allow direct operations on this compressed form without decompressing them. They represent Boolean functions as rooted, directed acyclic graphs with a number of intermediate nodes leading to terminal nodes. This is illustrated here:
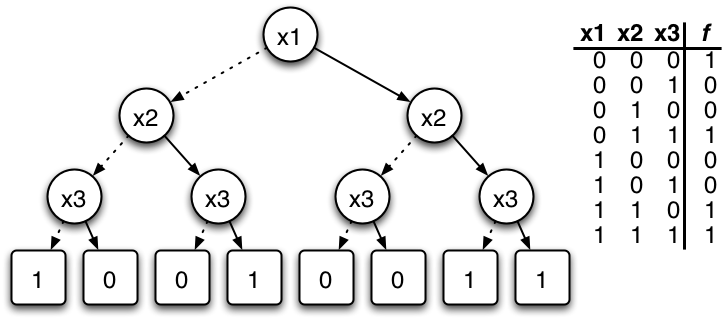
![]()
by this diagram of the function f:

In any case, I was unsure of why BDDs or MicroKanren are useful. Both articles seemed to aim at implementing their targets for little reason other than that these are new implementations. The Kanren project at least seems to aim at implementing a logic programming language which can be useful for some sorts of problems but BDDs seem like an unnecessarily complex construct whose purpose was not clear to me.
Learning and Teaching J
Array Thinking
Let's take a look at Pete Corey's blog entry "Now You're Thinking with Arrays".
He starts by saying that in spite of a few years of sporadic J usage, he still finds himself failing to grasp the “array-oriented” approach. However, he gives it another try with a problem of finding discrete differences between elements of a vector. That is, if discDiffs is the routine he wants, he should see something like this:
discDiffs 1 2 4 7 11 1 2 3 4
Pete takes a stab at the problem and comes up with an expression that works but seems overly complex.
(-/"1@:}.@:(],._1&|.)) 1 2 4 7 11 1 2 3 4
Seeking help, he posts a message on Twitter (does this seem odd to anyone besides me?) in #JLangTips. Based on this, he finds
2(-~/;._3) 1 2 4 7 11 1 2 3 4
This he calls "very nice" but is motivated to explore further. He gets this solution from someone named FireyFly:
(}. - }:) 1 2 4 7 11 1 2 3 4
I sent him an email explaining how to use prefix to accomplish this which seems the obvious way to me:
2-~/\ 1 2 4 7 11 1 2 3 4
How many J people use Twitter? Apparently not enough. Should we pay more attention to it?
The Value of a Good Community
Another J novice who blogs, Scott Locklin, had this to say a number of years ago. He had been looking for a time series database so naturally considered q and this led him to the other related array languages. He looked at Jdb because it was free and had some questions he posed to the J forum. He described his experience there like this:
I was expecting the usual dead language experience, but found a small, friendly and patient community of very smart people. Not the mixture of programmy smartness and smarm you’ll find in Lisp-land. These guys are math smart, stats smart, programmy smart, and just plain smart smart! I guess writing code that looks like line noise means, you have to be smart. They’re also extremely helpful. I mean, I asked a fairly n00b question, and got this in response. They didn’t just feed me a rote answer; they gave a damn if I understood what’s going on, and what the right way to do it was. No tinfoil helmeted one-true wayism involved. These fellas have a good tool; if you’re interested, they’ll show you how to use it. If you’re not, well, that’s OK too. They certainly seem to have a sense of humour; self-deprecation is a nice break from the galloping narcissism of many programmer communities.
Item of Interest
Paul Jackson will be giving a talk for APLBUG (APL Bay-area Users Group) on September 14th, 2020 at 10 AM PDT. He will speak about his experiences as an experienced APL programmer learning J.